Maddox Krape
Huffman Compression
Data Structures, Algorithms, and Encoding
History
Huffman compression, invented by David A. Huffman in 1952, revolutionized data encoding through its innovative variable-length prefix coding system. Inspired by a challenge from his MIT professor, Huffman developed an algorithm that efficiently allocated shorter codes to more frequently occurring symbols. This groundbreaking technique drastically reduced the average code length for messages, transforming the digital landscape and becoming widely adopted in various applications.
How does compression work?
File compression is the process of reducing the size of a file to save disk space and make it easier to transfer. One popular method for file compression is to use character frequency analysis, which takes advantage of the fact that some characters appear more frequently in a file than others. By replacing frequently occurring characters with shorter codes, the overall size of the file can be reduced without losing any of the original information.
Implementation (Part 1: Compression/Encoding)
- Determine the frequency (weight) of each character in the input data. Characters with more frequency have more "Weight"
- Create a leaf node for each character and add it to a priority queue based on its frequency.
- While there is more than one node in the queue, remove the two nodes with the lowest frequencies.
- Create a new internal node with the sum of the two removed nodes' frequencies as its weight. This new node becomes the parent of the removed nodes.
- Insert the new internal node back into the priority queue.
- Repeat steps 3-5 until there is only one node left in the queue, which becomes the root of the balanced Huffman tree.
- Traverse the tree from the root to each leaf node, assigning a binary code (0 or 1) to each edge along the path. The final code for each character is the sequence of edge codes followed from the root to the corresponding leaf node.
Weights in Huffman Compression refer to the frequencies of characters in the input data. The algorithm assigns shorter codes to more frequently occurring characters and longer codes to less frequent ones, resulting in an efficient compression scheme. To utilize a balanced tree, follow these steps:
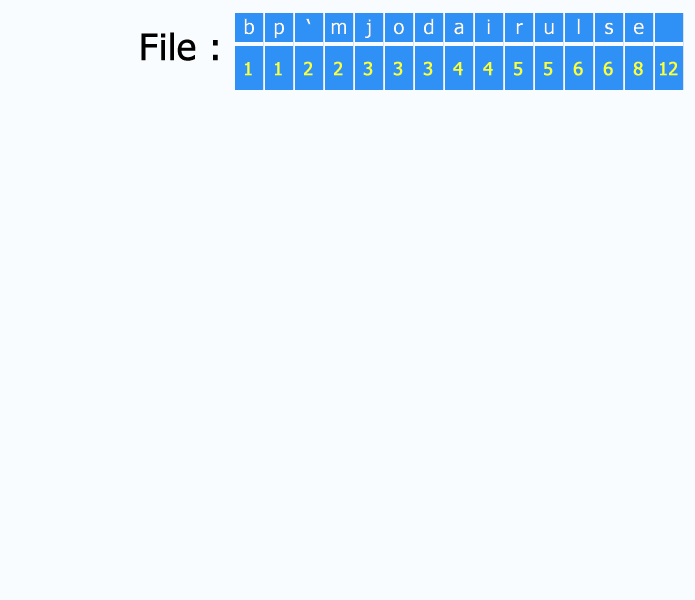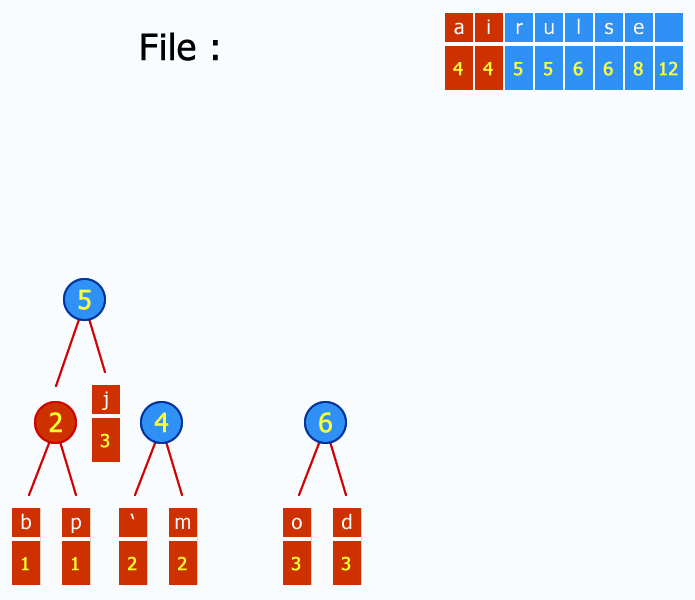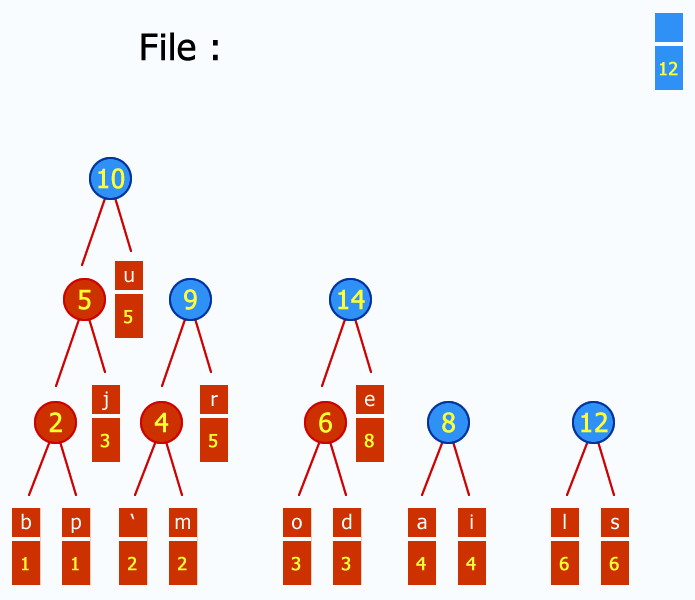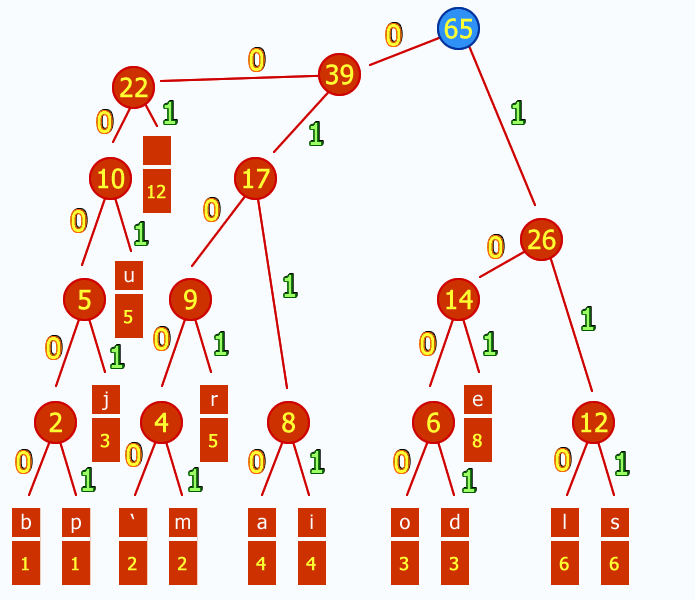
The following code successfully reads an ASCII file and produces the weights:
void generateWeights(String infName) {
// Open the input file
File inf = fio.getFileHandle(infName);
int status = fio.getFileStatus(inf, true);
// Make sure file is readable
if(readErrorCheck(status)) return;
// reset weights
initWeights();
BufferedReader br = fio.openBufferedReader(inf);
int c = 0;
try {
// Read the input file one character at a time until EOF
while ((c = br.read()) != -1) {
try {
weights[c]++;
} catch (ArrayIndexOutOfBoundsException e) {
// Ignore the character if it is not in the ASCII range
}
}
// Increment the count for the EOF character
weights[0]++;
br.close();
} catch (IOException e) {
e.printStackTrace();
}
outf = fio.getFileHandle(infName + ".csv");
saveWeightsToFile(outf.getName());
}The following code successfully takes the weights and file and builds a huffman tree
/**
* Builds the huffman tree. Make sure to:
* 1) initialize root to null (cleanup any prior conversions)
* 2) re-initialize the encodeMap
* 3) initialize the queue
* 4) build the tree:
* while the queue is not empty:
* pop the head of the queue into the left HuffmanTreeNode.
* if the queue is empty - set root = left, and return;
* pop the head of the queue into the right HuffmanTreeNode
* create a new non-leaf HuffmanTreeNode whose children are left and right,
* and whose weight is the sum of the weight of the left and right children
* add the new node back to the queue.
*
* It is assumed that the weights have been initialized prior
* to calling this method.
*
* @param minimize - This is just passed to the method to initialize the queue.
*/
void buildHuffmanTree(boolean minimize) {
HuffmanTreeNode left, right;
root = null;
encodeMap = new String[NUM_ASCII];
initializeHuffmanQueue(minimize);
while (!queue.isEmpty()) {
left = queue.poll();
if (queue.isEmpty()) {
root = left;
return;
}
right = queue.poll();
queue.add(new HuffmanTreeNode(left.getWeight() + right.getWeight(), left, right));
}
}
Implementation (Part 2: Uncompression/Decoding)
The main objective is to restore the original data from the compressed version. Here's an overview of how Huffman decompression works:
- Retrieve the Huffman tree: To decode a Huffman compressed file, you need the same Huffman tree that was used during the compression process. This tree is typically stored at the beginning of the compressed file, allowing the decompression algorithm to reconstruct the tree.
- Traverse the Huffman tree: Start at the root node of the Huffman tree. Read the compressed binary data bit by bit. If the bit is 0, move to the left child node, and if it's 1, move to the right child node.
- Identify the character: Continue traversing the tree based on the bits in the compressed data until you reach a leaf node, which represents a character in the original data. Append the character to the output.
- Repeat the process: Go back to the root node of the Huffman tree and continue reading the compressed binary data, traversing the tree, and appending characters to the output until you reach the end of the compressed data.
- Terminate the output: Some implementations use an End-of-File (EOF) marker to signal the end of the compressed data. When the EOF marker is encountered, the algorithm stops and the decompressed data is complete.
Key Takeaways
- Importance of data compression: Huffman compression is a widely used lossless data compression algorithm that highlights the significance of efficient data storage and transmission.
- Adaptive nature: The algorithm adapts to the input data, creating a unique Huffman tree and encoding for each file, which optimizes compression based on the frequency of characters in the data.
- Lossless compression: Huffman compression ensures that no information is lost during the process, allowing for accurate reconstruction of the original data during decompression.
- Binary tree structure: The use of a binary tree (Huffman tree) is a key aspect of this algorithm, as it enables efficient encoding and decoding of data.
- Greedy approach: Huffman coding employs a greedy algorithm, where the most frequent characters are assigned the shortest codes, resulting in optimal compression.
- Broad applications: Huffman compression is applicable in various fields, such as image and audio compression, text compression, and in some cases, network protocols like HTTP/2.
- Learning experience: Implementing Huffman compression and decompression algorithms provides valuable experience in understanding data structures, algorithms, and programming concepts.
You can browse the project on my Github: